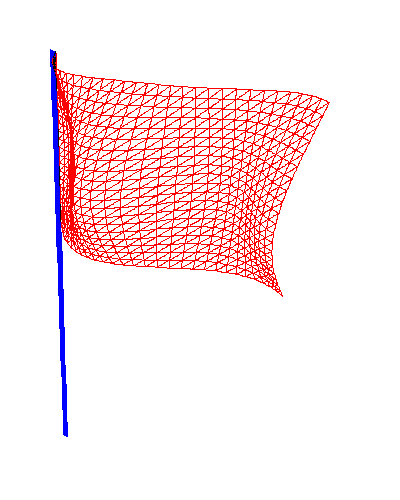
Flag Shader

Beispiel 5: Animation einer Flagge

Die Bedingungen einer richtigen Flagge sind , dass diese sich an einen Fahnenmast befestigen lässt und die Wind stärke zu- und abnehmen kann. Eine mathematische Funktion ist also grundlegend für das Verständnis der Bewegung einer Flagge.  Es ergibt sich eine komplexe Sinusformel die in den Vertex Shader ausgelagert wird und damit den Prozessor entlastet.

Erzeugen einer Sinuskurve mit MATLAB

Um die Bewegung der Flagge zu verstehen beginnen wir mit einer einfachen Sinuskurve.

Matlab File die Stauchung einer Sinuskurve: test1.m
x = 0:0.01:2pi;
z = sin(x);
plot(x,z,’b›);
axis equal
hold on
%location = -0.5;
%z = sin(x+location);
%plot(x,z,’r›);
wind = 2;
z = sin(windx);
plot(x,z,’g›)

Betrachten wir die Darstellung der 2 Sinuskurven  erkennen wir, dass eine Veränderung der Variablen wind, eine Stauchung  oder eine Streckung der Wellenlänge. In diesem fall wird die Wellenlänge  halbiert.

Gestauchte Sinuskurve:

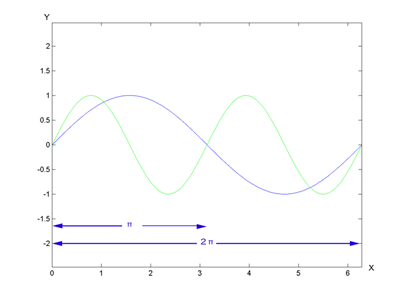
Diese einfache Sinuskurve reicht noch nicht aus um eine natürliche Flaggen Bewegung zu simulieren. Um eine bessere Bewegung zu erreichen,  bestimmen wir eine zweite Variable location. Diese änderbare Variable veranlasst den Ausschlag der Flagge.

Für die eigentliche Funktion wird eine mehrfache Sinus Multiplikation und Addition verwendet.

Matlab File ein Flaggen ähnliche Sinusmesh: flagge.m
[u,v] = meshgrid(0:0.1:2*pi+0.1,0:0.1:2*pi+0.1);
wind = 0.8;
location = 1;
X = u;
Y = v;
Z = sin(wind.*u).*sin(wind.*v) .* sin(location+u)+sin(wind .* u);

% Plot
mesh(X,Y,Z)
shading INTERP
axis equal

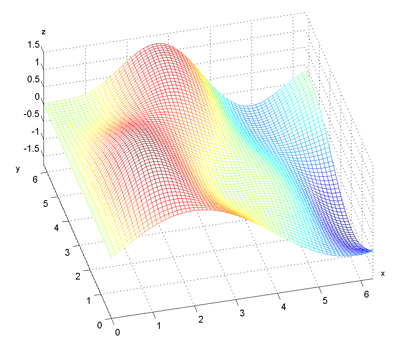
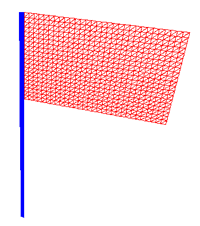
Darstellen einer Flagge mit OpenGL

Die Flagge wird aus einem rechteck mit F_Läge und F_Breite gebildet. Dieses Rechteck wird in viele kleine Quadrate unterteilt welche wiederum in Dreiecke halbiert werden. Die Quadrate bestehen aus den Eckpunkten a, b, c, d. Dieses Quadrat verschiebt sich in der Breite und Länge bis diese die Fläche der Flagge erstellt hat. Mit glVertex3f senden wir die einzelnen Vertexknoten dem Vertex Shader.

int F_Breite, F_Laenge; //Fahnen Breite und Länge
float ax, ay, bx, by, cx, cy, dx, dy; //Vertex Punkte eines 2D Quad
float r=0.2; //Quad Seitenlänge

F_Laenge = 30;
F_Breite = 20;

for (int i=0; i<F_Laenge; i++) //Meshzeichnen
{ for (int j=0; j<F_Breite; j++)
{
ax = ir; //Algorithmus für die Verschiebung ay = jr; // der einzelnen Vertex Punkte des Quad bx = (i+1)r; by = ay; cx = (i+1)r;
cy = (j+1)r; dx = ax; dy = (j+1)r;

glColor3f(1.0,0.0,0.0); //Flagge wird Rot gefärbt glBegin(GL_TRIANGLES); //Die einzelnen Quads //werden als Dreiecke aufgebaut

glVertex3f(ax, ay, 0.0f);
glVertex3f(bx, by, 0.0f);
glVertex3f(cx, cy, 0.0f);
glVertex3f(cx, cy, 0.0f);
glVertex3f(dx, dy, 0.0f);
glVertex3f(ax, ay, 0.0f); glEnd();
}}

Verwenden des Vertex Shaders für die Flagge.

Hier erkennern wird den Grund weshalb Matlab als Einführung verwendet wurde, denn ohne diese ist es schwer zu erkennen was diese Sinusfunktion macht. Die erste, hier auskommentierte Sinusfunktion bewirkt die Stauchung der Fahne. Die zweite, etwas komplexere Funktion unterstützt die natürliche Flaggen bewegung

Source code: simple.vert

uniform float location;
uniform float wind;
varying vec4 color; void main(void)
{
vec4 a = gl_Vertex; // a ist eine schreibbare kopie von gl_vertex

//a.z = sin(winda.x)sin(wind*a.x + location); //Fahne stauchen

a.z =sin(winda.x)sin(winda.y)sin(location+a.x)+sin(wind*a.x); //Fahne weht und flattert
gl_Position = gl_ModelViewProjectionMatrix * a;
color = gl_Color;
}