Licht Shader
Licht Shader Programmierung
Wir verwenden hier vier Lichter die auf eine Kugel gerichtet sind. Die Deklaration und die Einbindung der beiden verwendeten Shader steht in der FragmentLightingShader2 Klasse. Die Ausgabe findet mit Hilfe eines Qt Widget statt, d.h. auch die Übergabe der beiden Parameter int argc, char** argv, bei main() . Die Lichter werden einzeln erzeugt und im Fragmet Shader einzeln abgefragt. Es muss eine Instanz der FragmentLightingShader2 Klasse erzeugt werden.
Übergabe der Parameter an den Shader innerhalb des main.
scene->addNode(new SLAppearance (SLCol4f(1.0,1.0,1.0,1),SLCol4f(1,1,1,1),100,0, &Flightshader2)); scene->addNode(sphere);
Beenden des Shader
scene->addNode(new SLAppearance(SLCol4f(), SLCol4f(), 0, 0, 0));
Licht Shader – Vertex Shader Programmierung
Dies ist eigentlich in diesem Beispiel nicht relevant, da ein Per Fragmentlighting um einiges besser dargestellt wird. Mittels Per Framgmentlighting werden auch Fragmente belichtet die innerhalb der verschiedenen Vertex Punkte liegen. Es werden hier keine wichtigen Berechnungen durchgeführt. Der Vertex Shader ist nur für die Ansichtsmatrix zuständig und für die Übergabe der einzelnen Punkte P (Vertex), n ist die Normalisierte der Normalen N. d.h. haben wir hier auch das kleine n verwendet. Anhand der varying Variabeln können wir die beiden berechneten Werte P und n dem Fragment Shader übergeben. Unten ist der ganze Inhalt des Vertex Shader Programms aufgelistet.
F_lighting2.vert
varying vec3 n;
varying vec3 P;
void main(void)
{
P = vec3(gl_ModelViewMatrix * gl_Vertex);
n = normalize(gl_NormalMatrix * gl_Normal);
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
Licht Shader – Vertex Shader Programmierung
Im Fragment Shader F_lighting2.frag wird die eigentliche Beleuchtung berechnet. Hier ist wichtig, dass man die Vektormathematik verstanden hat.
Einführung in die Mathematik der vektorbasierten Licht- und Reflektionsgesetz
Wenn ein Lichtstrahl L auf eine Oberfläche fällt, wird dieser zu unserem Auge E reflektiert. Halbiert man den Winkel zwischen dem Lichtstrahl L und dem Eye Vektor findet man die Winkelhabierende H. Die Normale N steht senkrecht auf der Oberfläche unseres beleuchteten Objekts. Aus der Physik wissen wir, dass der Lichteinfalls Winkel mit dem gleichen Winkel an der Normalen gespiegelt wird, diesen Reflektierte Lichtstrahl nennen wir R. R ist in der unteren Grafik nicht eingezeichnet.
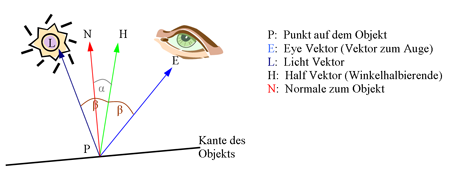
Im Fragment Shader F_lighting2.frag werden zu erst alle Variabeln deklariert. Danach werden für die vier Lichtquellen die Vektoren berechnet.
Normale
N = normalisierte von n (n wurde im Vertex Shader berechnet).
Licht Vektor
L = normalisierter Abstand des Lichtes zum Punkt P.
Die einzelnen Lichtpos. und der Punkt P sind bekannt und somit mit
L = Lichtpos – P zu berechnen.
Eye Vektor
E = normalisierter und invertierter Vektor von P. Die Koordinaten der beiden Punkte E und P sind gegeben. Der Vektor muss invertiert werden damit er von P nach E zeigt.
R = normalisierter Licht Vektor L an der Normalen N gespiegelt. L und N sind gegeben, d.h. wird R mit der Funktion reflect() berechnet. R muss invertiert werden damit die Richtung des Vektors stimmt.
H = normalisierter Half Vektor von den Vektoren E+L.
Wichtig für die Darstellung ist die Lichtstärke, die mit zunehmender Distanz zum Objekt abnimmt. Diese abnahm der Lichtstärke wird als attenuation beschrieben. Es wird die konstante, lineare und quadratische Abnahme berücksichtig. C sind die konstante und d steht für die Distanz.
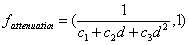
Danach wird mit Spotdot kontrolliert, ob der Vertex
Punkt P innerhalb des Lichtkegels liegt. Dies wird mit dem
Punktprodukt(dot) von L und der Spotrichtung der einzelnen Lichtquelle
berechnet. Falls der Punkt P ausserhalb des Lichtkegels liegt, muss
dieser nicht berücksichtigt werden, andernfalls muss er berechnet
werden.
Es werden noch die verschiedenen Lichtreflexionen, wie das Ambiente-, Diffuse- und Speculärelicht benötigt.
Das Ambientelicht wird mit der Formel berechnet: Iambient=Ie*ke
mit Ie als konstante, ambiente Lichtintensität und mit ke als ambiente Reflexionskoeffizienten.
Das Diffuselicht wird mit der Formel berechnet:

mit Id als konstante, diffuse Lichtintensität, mit Kd als diffuse Reflexions-koeffizienten (zwischen 0 und 1) und der Berechnung des Puntproduktes von N und L.
Das Speculärelicht (spiegelndes Licht) wird mit der Formel berechnet:
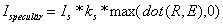
Diese Formel stammt von Bui-Thong Phong.
mit Is als konstante, speculäre Lichtintensität, mit Ks als speculäre Reflexionskoeffizienten (zwischen 0 und 1) und der Berechnung des Puntproduktes von R und E.
F_lighting2.frag
varying vec3 n;
varying vec3 P;
void main (void)
{
int i; vec3 L; vec3 E; vec3 R; vec3 H; vec3 N; float distance;
float SpotEffect;
float attenuation;
vec4 Iamb ;
vec4 Idiff;
vec4 Ispec;
float SpotDot;
for( i=0; i < 4; i++)
{
N = normalize(n);
L=normalize(gl_LightSource[i].position.xyz-P);
E = normalize(-P);
R = normalize(-reflect(L,N));
H = normalize(E+L);
distance = length(L);
//Distanz des Lichtes auf den Vertex SpotEffect;
//abnahme
attenuation= 1.0 / (gl_LightSource[i].constantAttenuation + gl_LightSource[i].linearAttenuation *distance + gl_LightSource[i].quadraticAttenuation *distance *distance); //Spott berechnung ob p innerhalb oder //ausserhalb Lichtkegel
SpotDot = dot(-L, gl_LightSource[i].spotDirection);
if (SpotDot < gl_LightSource[i].spotCosCutoff)
SpotEffect = 0.0;
else
SpotEffect = pow(SpotDot, gl_LightSource[i].spotExponent);
Iamb = gl_FrontLightProduct[i].ambient;
Idiff = gl_FrontLightProduct[i].diffuse * max(dot(N,L), 0.0);
Ispec = gl_FrontLightProduct[i].specular * pow(max(dot(R,E),0.0),0.3 * gl_FrontMaterial.shininess);
gl_FragColor += Iamb + attenuation * SpotEffect * (Idiff + Ispec);
} }
Ispec mit Blinn Shader
vec4 Ispec =
gl_FrontLightProduct[i].specular * pow(max(dot(N,H), 0.0), gl_FrontMaterial.shininess);