Arbeitsauftrag
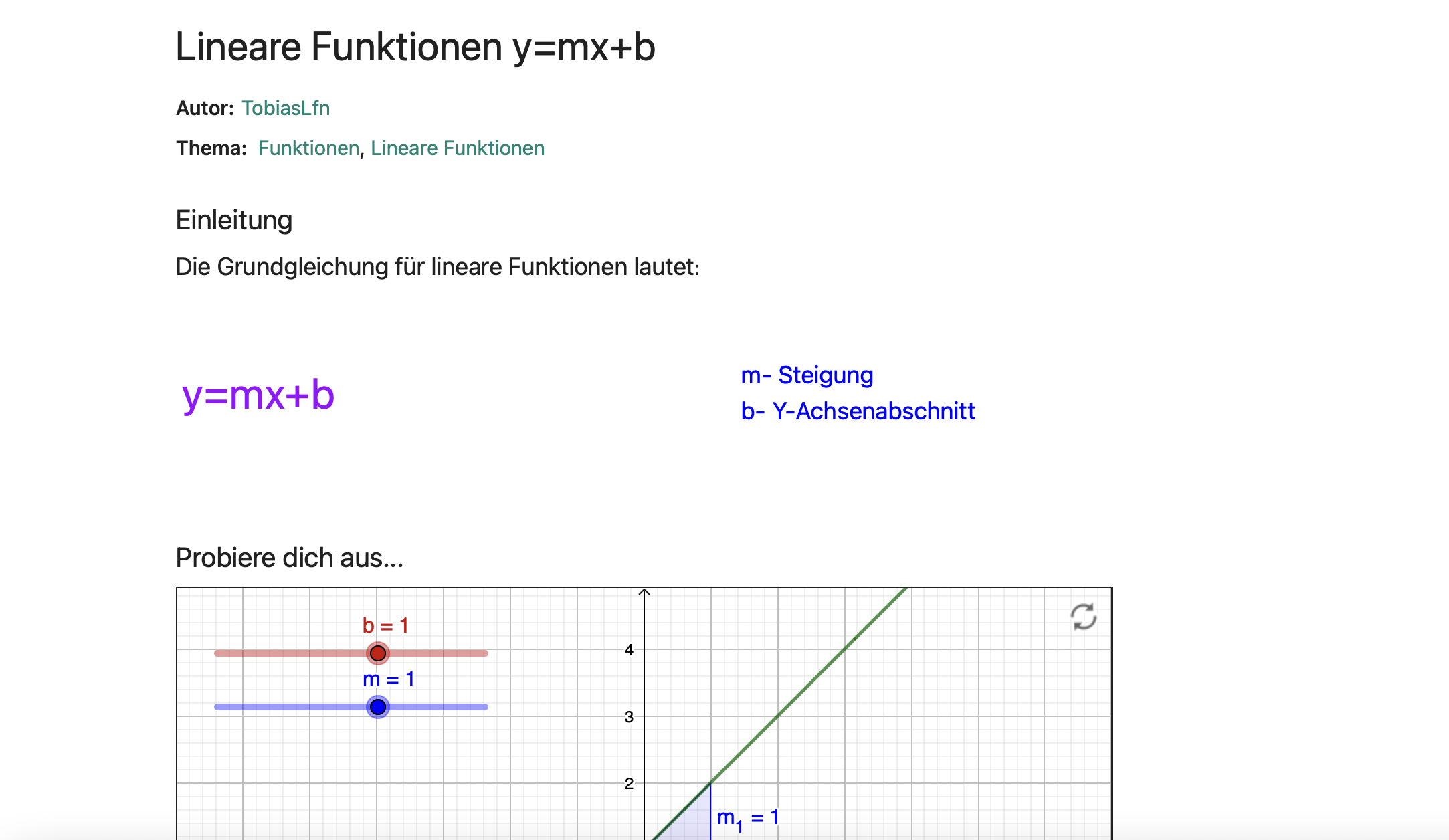
Einleitung Die Grundgleichung für lineare Funktionen lautet:         y=mx+b   m- Steigung  b- Y-Achsenabschnitt Probiere dich aus... Steigung Die Steigung m gibt an, um wie viele y-Einheiten () sich der Graph der Funktion im Verhältnis zur Änderung der x-Einheiten () ändert. Wie steil oder flach der Graph der Funktion steigt/fällt. Allgemeine Formel: m= Steigungsdreieck Das Steigungsdreieck ist die grafisch Darstellung der Steigung der Funktion. Auch an dem obrigen Graph einer Funktion ist ein blaues Steigungsdreieck. Abbildung Steigungsdreieck Abb.1.1 In der Abbildung ist eine Funktion erkennbar, an der ein Steigungsdreieck anliegt. Du siehst, dass sich der Graph der Funktion um eine x-Einheit () nach rechts und um eine y-Einheit () nach oben bewegt. Wenn du die Werte in die Formel m= einsetzt, so erhälst du eine Steigung von m=1. Y-Achsenabschnitt Der y-Achsenabschnitt b gibt an, an welcher Stelle der y-Achse der Graph der Funktion diese schneidet.

Ergänzungen

Lernziel
Erkunden und Verstehen von Lineare Funktionen y=mx+b